Harmonic tones
Harmonics are naturally occuring when a string is vibrationg or when you are blowing a trumpet. In the animation you can se how the string is vibrating in 3 different modes. The string can also vibrate with 4,5,6,7.... mode. These are called harmonics. The same thing happens with the air column of a flute or trumpet. The famous frensh mathematician Fourier proved that all peridic oscillations can be divided into a number of sine kurves, that are harmonic with the root period. That is all tones (that are not exactly sine formed) will have harmonics that are multiple of the root frequency.
Two notes sound well when the overtones are coinsiding. By experiementing the old greeks found that the intervals where the string length were related with the formula (1-n)/n: 2/1, 3/2, 4/3, 5/4, 6/5,7/6,8/7,9/8,10/9 where sounding well together.. These relations are called (1+n)/n or epimoric relations. Although the ancient greeks failed to defined the concept of frequency, they described the frequency relationship of harmonics.
The were using harp like instruments (Lyra and Khithara) without fingerboard, and they started their scale (or tonoi) from the high pitch and when down. Therefore the relation found describes a frequency relation. (although we know that the frequency is inversly related to the string length - but they used the inverse string length relation by starting from above hence they got the frequency relation.
The lower the epimoric ration the more consonant interval.
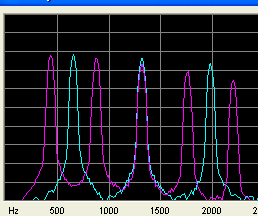
Frequency spectrum of the two notes A 440,0 Hz and E 660,0 Hz the second harmonic of 660 Hz coincides with the third harmonic of the A.
